According to a popular 2017 review by famous researchers Robert Siegler and David Braithwaite there are certain deep-rooted and fundamental cultural differences and curricular exigencies that make learning arithmetic difficult for learners from one country to another. Cross-culturally, problems in math learning arise especially during the phase when learning properties of whole numbers are extended to include all other types of numbers. Two particular concepts; (1) Numerical magnitudes and (2) Rational number arithmetic, and how well teachers understand and teach these are critical to our own mastery of numbers. This is regardless of how intelligent we are and irrespective of our linguistic or mathematical ability. The present post is an attempt to elucidate these findings.
When do we start learning whole numbers and fractions?
The average child between three and five years has no difficulty in picking up numbers from zero to ten, which extends to 100 by seven years and beyond 1000 by twelve years. Fractions between 0 and 1 are picked up around eight years of age, while all other fractions are learnt post eleven years of age
By Damien Karras (Own work), via Wikimedia Commons
What is numerical magnitude and rational number arithmetic?
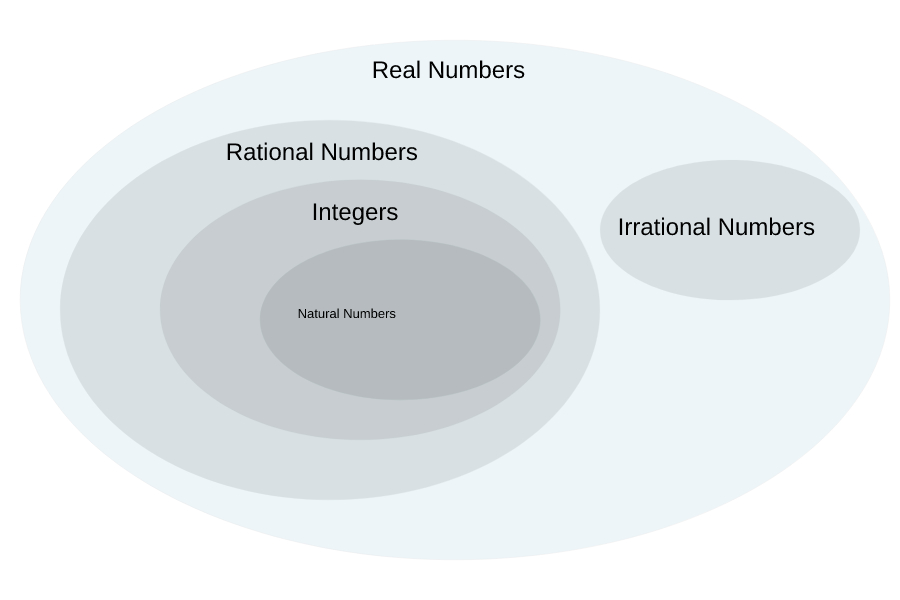
(1) Numerical magnitude understanding means the ability to comprehend, gauge (order) and compare the sizes of numbers (whole numbers as well as fractions). Such representations form the basics of math learning and are applicable in real-life. Known as the Weber-Fechner law of perception, mastery over numerical magnitudes gets generalized into real life situations where discrimination between two numbers becomes increasingly difficult as the difference between them decreases. The “distance effect” as it is called is seen when for instance, one is shopping around for discounts. While one might travel up and down a department store to get a large percentage discount on small items, one won’t make a similar effort on very large purchases where smaller percentage discounts are offered. In short, one fails to compare the absolute rupee amount saved when comparing the aforementioned two cases.(2) Rational number arithmetic comprises ratios of numbers expressed as fractions. Whereas neuroscience data from several experiments locate similar areas of the brain where processing of fraction and whole number magnitudes takes place, there are problems that arise during the learning process when properties of whole numbers are generalized to all other types of numbers.
Why cant one generalize properties of some numbers (natural, whole, integers) to all other (rational) numbers?
In order to demonstrate this idea we present a few problems.
(1) In contrast to whole numbers that are represented with one single symbols (such as “2” for two), fractions can be represented in several different ways (1/2 or 2/4 or 3/6).
(2) When one multiplies natural numbers like 2 x 3, the product is always larger than either 2 or 3, this is not the case however when you multiply numbers between 0 and 1 (1/2 x 1/2 = 1/4).
(3) Similarly if you add whole numbers (0 + 2 = 2), the resulting number is never smaller than either addend, however this is not the case while adding negatives.
What is the point I am making?
Lewis Carroll, via Wikimedia Commons
“And as in uffish thought he stood,
The Jabberwock, with eyes of flame,
Came whiffling through the tulgey wood,
And burbled as it came!”

Rational number arithmetic is something that is hoisted upon unsuspecting 8 year olds, who see it as one does the nonsensical poem Jabberwocky by Lewis Caroll. Teachers must decode both the logic and language of this math through a process of guided discovery and play, but above-all encouragement for their students. To those students who, like me, have unfortunately endured unkind or obnoxious math teachers at some junction, I leave you with a continuation of part of a quote by Chef.Auguste Gusteau from Pixars animation Ratatouille,
“You must be imaginative, strong-hearted. You must try things that may not work, and you must not let anyone define your limits”
In todays day and age of information dissemination via the internet, the sky is literally the limit.